Appendix X: Common Probability Distributions
A wide variety of probability distributions are available for modeling cost risk and uncertainty. The triangular, lognormal, beta, uniform, and normal distributions are the most common distributions that cost estimators use to perform a risk and uncertainty analysis. They are generally sufficient, given the quality of the information derived from interviews and the granularity of the results. However, many other types of distributions are discussed in cost estimating literature and are available through a variety of estimating tools. The shape of the distribution is determined by the characteristics of the risks they represent. If they are applied to WBS elements, they may combine the impact of several risks, so it may take some thought to determine the most appropriate distribution to use. Table 48 lists the five most common probability distributions used in risk analysis.
Table 48: Common Probability Distributions
| Distribution | Description | Shape | Typical application |
|---|---|---|---|
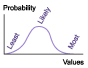
| Beta | Similar to normal distribution but does not allow for negative cost or duration, this continuous distribution can be symmetric or skewed |
|
To capture outcomes biased toward the tail ends of a range; often used with engineering data or analogy estimates; the shape parameters usually cannot be collected from interviewees |
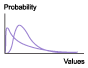
| Lognormal | A continuous distribution positively skewed with a limitless upper bound and known lower bound; skewed to the right to reflect the tendency toward higher cost |
|
To characterize uncertainty in nonlinear cost estimating relationships; it is important to know how to scale the standard deviation, which is needed for this distribution |
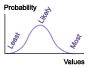
| Normal | Used for outcomes likely to occur on either side of the average value; symmetric and continuous, allowing for negative costs and durations. In a normal distribution, about 68 percent of the values fall within one standard deviation of the mean |
|
To assess uncertainty with cost estimating methods; standard deviation or standard error of the estimate is used to determine dispersion. Because data must be symmetrical, it is not as useful for defining risk, which is usually asymmetrical, but can be useful for scaling estimating error |
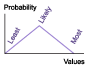
| Triangular | Characterized by three points (most likely, pessimistic, and optimistic values) can be skewed or symmetric and is easy to understand because it is intuitive; one drawback is the absoluteness of the end points, although this is not a limitation in practice since it is used in a simulation |
|
To express technical uncertainty, because it works for any system architecture or design; also used to determine schedule uncertainty |
| Uniform | Has no peaks because all values, including highest and lowest possible values, are equally likely |
|
With engineering data or analogy estimates |
Source: DOD and NASA. | GAO-20-195G